Spherical or omni-directional images offer an immersive visual format appealing to a wide range of computer vision applications. However, geometric properties of spherical images pose a major challenge for models and metrics designed for ordinary 2D images. Here, we show that direct application of Fréchet Inception Distance (FID) is insufficient for quantifying geometric fidelity in spherical images. We introduce two quantitative metrics accounting for geometric constraints, namely Omnidirectional FID (OmniFID) and Discontinuity Score (DS). OmniFID is an extension of FID tailored to additionally capture field-of-view requirements of the spherical format by leveraging cubemap projections. DS is a kernel-based seam alignment score of continuity across borders of 2D representations of spherical images. In experiments, OmniFID and DS quantify geometry fidelity issues that are undetected by FID.
Spherical images, projections, and generative modelling
Spherical images, offering a full 360-degree horizontal and 180-degree vertical field of view, hold immense potential for a broad range of computer vision applications such as virtual reality, game design and immersive panoramic image viewing.
However, spherical images have geometric properties not exhibited by regular 2D images, and most datasets are not representative of this format of images. Consequently, most existing models are not directly applicable or optimized for spherical images.
To reduce this challenge, we can project between a spherical 3D image and 2D representations of it. Importantly, models applied on such representations must be aware of the inherent projection distortions in order to adhere to the geometric constraints of the 3D sphere.

FID is insufficient
Fréchet Inception Distance (FID) is a popular metric for evaluating realism by comparing image distributions. Typically, one compares an image dataset generated by a model with a representative reference set, e.g. the training set for the model. FID has in many ways become the de-facto standard metric for comparing generative models, both for regular image and now spherical image generative models.
However, we demonstrate that FID, being reliant on a convolutional neural network backbone trained on ordinary images, is not capable of detecting distortions that tamper with spherical image geometry. This is a serious limitation of the metric for spherical images, as the metric is not sufficient to detect if a model is able to generate valid spherical images.
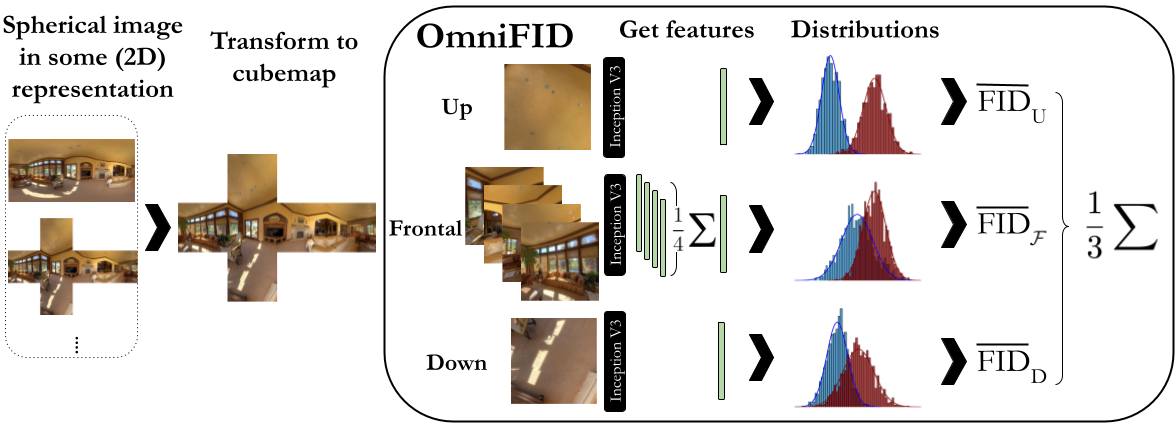
OmniFID and Discontinuity Score
To address this issue, we first propose an extension of FID, which we term Omnidirectional FID, or OmniFID. Since FID has useful and empirically proven qualities, we wish to adjust the metric itself minimally, and instead focus on adapting the data to be more compatible with metric.
For this, we propose using alternative projections (so-called cubemaps). These projection produce six viewpoint 2D images rather than a single global 2D image. Although this splits semantic information across images, the viewpoint images better display any potential issues with geometry - in particular for the up- and downwards views, as the spherical poles are especially distorted. Based on semantics, we group images and average FID scores over the groups, resulting in our proposed OmniFID metric.
For any 2D projection of the sphere, continuity across image borders must be guaranteed. Otherwise, visible seams will appear when the spherical image is rendered. To address this we propose the Discontinuity Score (DS), a simple kernel-based metric. We show that DS scores severe semantic misalignments and smaller inconsistencies in a satisfactory manner.

Want to know more?
For more details, background, and analysis, please check our paper to be published in ECCV 2024! It is available at https://arxiv.org/abs/2407.18207. A reimplementation of the code will be made available at https://github.com/Anderschri/OmniFID.