EML Munich

Disentangled Representation Learning with the Gromov-Monge Gap

Théo Uscidda*, Luca Eyring*, Karsten Roth, Fabian J Theis, Zeynep Akata*, Marco Cuturi*

International Conference on Learning Representations, ICLR

2025

Abstract

Learning disentangled representations from unlabelled data is a fundamental challenge in machine learning. Solving it may unlock other problems, such as generalization, interpretability, or fairness. Although remarkably challenging to solve in theory, disentanglement is often achieved in practice through prior matching. Furthermore, recent works have shown that prior matching approaches can be enhanced by leveraging geometrical considerations, e.g., by learning representations that preserve geometric features of the data, such as distances or angles between points. However, matching the prior while preserving geometric features is challenging, as a mapping that fully preserves these features while aligning the data distribution with the prior does not exist in general. To address these challenges, we introduce a novel approach to disentangled representation learning based on quadratic optimal transport. We formulate the problem using Gromov-Monge maps that transport one distribution onto another with minimal distortion of predefined geometric features, preserving them as much as can be achieved. To compute such maps, we propose the Gromov-Monge-Gap (GMG), a regularizer quantifying whether a map moves a reference distribution with minimal geometry distortion. We demonstrate the effectiveness of our approach for disentanglement across four standard benchmarks, outperforming other methods leveraging geometric considerations.

The Problem: Geometry Preservation vs. Prior Matching

Recent studies have shown that incorporating geometric constraints on representation spaces can enhance disentanglement. These approaches encourage latent representations to preserve key geometric features of the data, such as distances or angles between samples.

To quantify this preservation, we can use the distortion (DST) of a map T, which measures how much T distorts geometric features encoded by cost functions $c_\mathcal{X}$ and $c_\mathcal{Y}$ with respect to reference distribution $r$ :

\begin{equation} \mathrm{DST}_r(T) := \int_{\mathcal{X}\times \mathcal{X}} \tfrac{1}{2} (c_\mathcal{X}(\mathbf{x},\mathbf{x}') - c_\mathcal{Y}(T(\mathbf{x}), T(\mathbf{x}')))^2 \mathrm{d}r(\mathbf{x})\mathrm{d}r(\mathbf{x}')\,. \end{equation}

When this distortion equals zero, the map perfectly preserves the geometric features. However, this approach faces a fundamental challenge: in general, a mapping that perfectly aligns the data distribution with the prior while fully preserving these geometric features may not exist.

As illustrated in the figure above, when trying to map from a source distribution (left) to a target distribution (middle), we encounter a trade-off. Without regularization, we match the target but don't preserve geometric structure (third column). Using the distortion (DST) as a regularizer forces geometric preservation but fails to match the target distribution (fourth column). What we need is an optimal compromise.

The Solution: Gromov-Monge Gap (GMG)

Instead of seeking a distortion-free map, we propose to find a map that transports the reference distribution with minimal distortion. This is precisely what Gromov-Monge maps achieve in optimal transport theory—they transport one distribution onto another while preserving geometric features as much as possible.

The key innovation is the Gromov-Monge Gap (GMG), a regularizer that quantifies whether a map transports a reference distribution with minimal geometry distortion. The GMG measures the difference between:

The actual distortion incurred when transporting a distribution with a given map
The minimal possible distortion achievable when transporting the distribution

To quantify how close a map T is to being a Gromov-Monge map, we introduce the Gromov-Monge Gap (GMG):

\begin{equation} \mathrm{GMG}_r(T) := \mathrm{DST}_r(T) - \mathrm{GW}(r, T\sharp r) \end{equation}

where $\mathrm{GW}(r, T\sharp r)$ is the Gromov-Wasserstein distance between $r$ and $T\sharp r$ , representing the minimal distortion achievable when transporting $r$ to $T\sharp r$ .

The GMG can be understood as a "debiased distortion." It compares the distortion induced by T to a baseline distortion defined as the minimal achievable distortion. When transformation without distortion is achievable, this baseline becomes zero, and the GMG equals the distortion. Otherwise, the GMG avoids over-penalizing maps when full preservation is impossible.

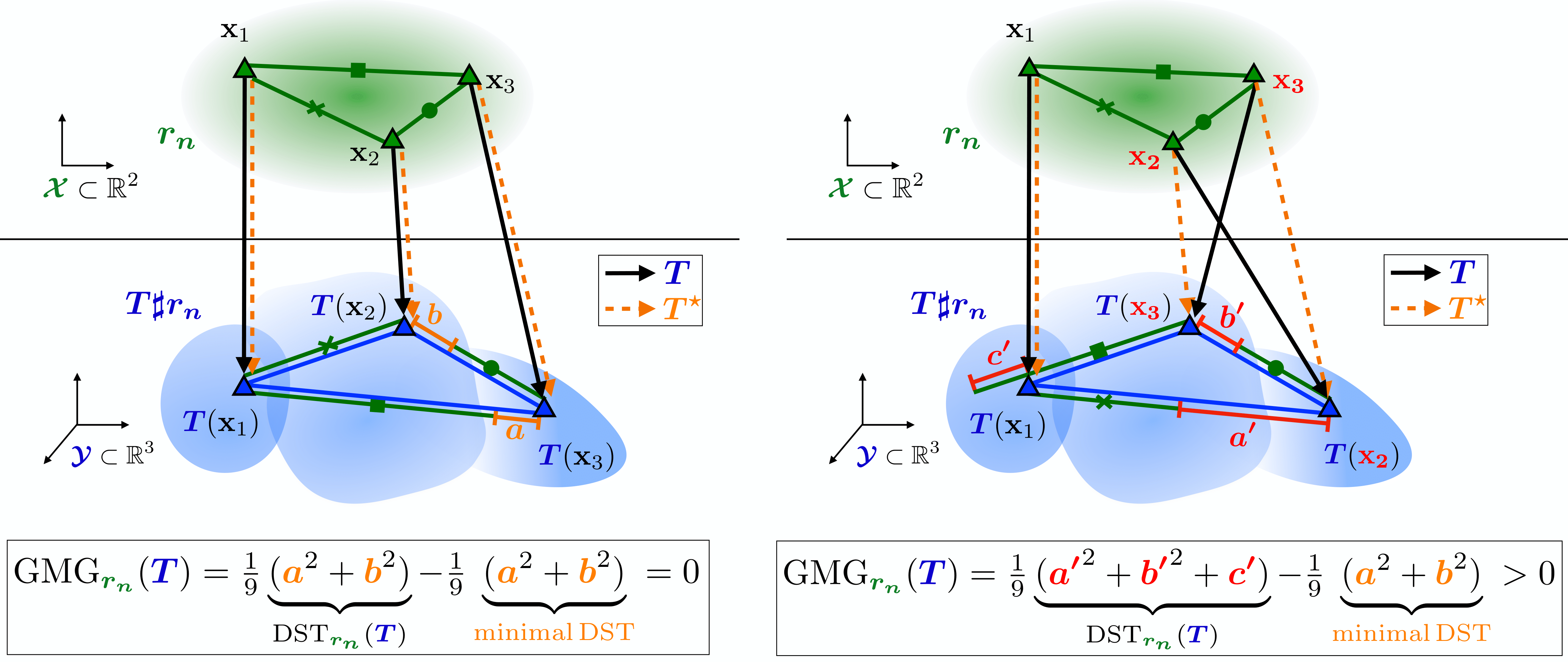
Figure 1: Sketch of GMG for two different maps T. Using a discrete reference distribution on 3 points, the method measures if T minimally distorts the distances. On the left, T is the optimal map, mapping three points with minimal (yet non-zero) distortion (GMG = 0). On the right, T swaps two points compared to the optimal map, causing higher distortion than minimal (GMG > 0).

As shown in the fifth column of the first figure, using the GMG as a regularizer provides the optimal compromise: it matches the target distribution while preserving geometric features as much as possible.

Key Advantages of GMG

The GMG offers several advantages over existing approaches:

Optimal compromise: It finds the best possible mapping that aligns distributions while preserving geometric features as much as possible
Flexibility in features: It works with various geometric features like scaled distances or angles between points
Theoretical guarantees: We prove that GMG and its finite-sample counterpart are weakly convex functions, characterizing the convexity constants and their practical implications
Computational efficiency: The method can be implemented efficiently using existing optimal transport solvers, with complexity scaling linearly with the dimensions of the source and target spaces

Results and Performance

We demonstrate the effectiveness of our approach on four standard disentanglement benchmarks, including Shapes3D, DSprites, SmallNORB, and Cars3D. The results show that:

GMG consistently outperforms standard distortion metrics
Angle preservation (using cosine similarity) performs better than distance preservation
Decoder regularization yields stronger results than encoder regularization
The GMG provides more stable gradients compared to standard distortion metrics
The approach shows robust performance across different datasets and base VAE methods

Conclusion

The Gromov-Monge Gap introduces a novel perspective on disentangled representation learning through optimal transport theory. By finding an optimal compromise between distribution matching and geometry preservation, it achieves more effective disentangled representations. For detailed results, theoretical guarantees, and implementation details, we refer readers to our full paper.